Let’s explore the mathematical model for optimizing the tradeoff between errors and rejects.

The reject mechanism helps to guarantee the specified error level required by an application. Recognition engines usually return an answer accompanied by a value parameter called confidence value. The confidence value ranges from 0 to 100 and indicates how confident the engine is that a particular answer is correct. If the engine is less confident that a recognition result is correct (confidence value is below the chosen threshold), the result can be rejected. Confidence values provide a flexible, controllable mechanism that allows tuning for specific needs. For example, if an application cannot tolerate an error rate higher than 1%, it is possible to choose a confidence value threshold so that answers accepted by the system as correct will contain no more than 1% errors (on average or with high probability). Those applications that are less sensitive to error rate but instead have a requirement to minimize expenses associated with data processing can use the reject mechanism to trade errors for rejects, i.e. to set up a solution that provides the biggest savings.

The best and most accurate ratio between errors and reject is chosen using the following mathematical model. Both reject and error rate are functions of the confidence level threshold. Since rejects depend on the confidence level threshold monotonically, error rate could be considered to be a function of reject. This function is called reject curve.

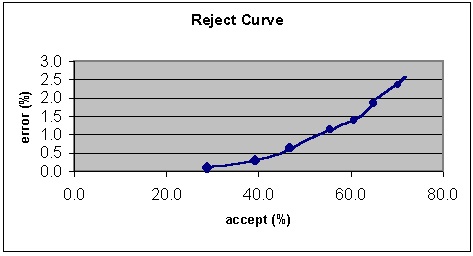
Sample error-reject curve. Each dot on the graph is associated with a certain confidence value that may be chosen as a threshold value. The higher the selected threshold level, the lower the number of errors in the accepted results.

At each specific point of the curve reflecting dependence of error rate from reject rate there is an error ratio which reflects how many items should be rejected to eliminate 1 error or how many items will be excluded from reject if we permit it to make additional errors. Usually it is expressed as 1:N (one error for N rejects). In many applications, N is chosen in the range from 2 to 10. Mathematically this ratio is minus a derivative of a function “Errors from Rejects”. If there is a processing cost associated with handling errors and a cost associated with handling rejects, the best choice for error rate versus reject rate corresponds to the point where this ratio is equal to the ratio between cost of rejects and the cost of errors.